Pressure drop
Pressure drop in tube systems

Determining the pressure drop is essential for the overall system design and specification of the pumps.
The pressure drop can be determined with measurements within the real system - it often is better to identify the pressure drops in the planning phase.
The calculation of the pressure drops in tube systems is described in the following.
The CONEXA engineering team will be gladly at your service when you encounter any questions.
Laminar or turbulent flow
The determination of the pressure drop greatly depends on wether the flow is laminar or turbulent. The tube friction factor is calculated with two different formulas, depending on wether a laminar or turbulent flow is present. The tube friction factor is calculated with two different formulas, depending on wether a laminar or turbulent flow is present.
Laminar Flow | = | Reduced pressure drop |
Turbulent Flow | = | Significantly increased |
Calculation of the Reynolds' number:
$$\displaystyle Re = {{c*d} \over {\nu(T)}}$$
| Reynolds' number Re < 2320 laminar flow | Reynolds' number Re > 2320 turbulent flow |
Calculation of tube friction factor λ : | |
$$\displaystyle\lambda = {64 \over Re}$$ (with Re < 2320) | $$\displaystyle\lambda = {0.3164 \over \sqrt[4]{Re}}$$ (with Re ≥ 2320) |
The pressure drop inside the tube is specified with the value delta-p while it is computed as follows:
$$\displaystyle\Delta p = \lambda * {L \over d} * {{p(T) * c^2} \over 2} \text{[Pa]}$$
Individual resistance of the components in the system
The total pressure drop is the sum of the pressure drop in the tubes and the pressure drop of the different components in the system. The individual pressure drop of the different components is determined with the following characteristic values:
Calculation of the individual pressure drop:
$$\Delta p = \zeta * \rho(T)*{c^2 \over 2} \text{ [Pa]}$$
The pressure drop coefficients for the different components are specified in the following. They are the average values for the entire type.
Pressure drop coefficient for bends
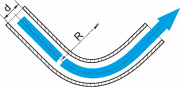
The pressure drop depends on the ratio of the inner diameter to the radius of the bend:
| Radius / diameter | Drag coefficient |
|---|---|
| $${R \over d} = 2$$ | $$\zeta = 0.21$$ |
| $${R \over d} = 4$$ | $$\zeta = 0.14$$ |
| $${R \over d} \leq 6$$ | $$\zeta = 0.11$$ |
Pressure drop coefficient for straight fittings

e.g.: C-G, C-GE, C-EGE
The pressure drop for straight fittings is minimal or even negligible.
In general one can assume the following pressure drop coefficient:
Straight fitting:
$$\zeta = 0.01 \text{ ... } 0.05$$
Pressure drop coefficient for reducers
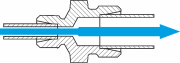
Pressure drop coefficient for reducers, extension in direction of the flow
e.g.: C-RED, C-GR, C-KOVO
The pressure drop coefficient of extensions with a reduction in direction of the flow is determined as follows:
$$\zeta = ({A_2 \over A_1} - 1)^2$$
A₁ = Area of the opening
A₂ = Area of the exit
Specifying a value here does not make sense due to the fact that the pressure drop coefficient can be anywhere between 1.5 and 5000.
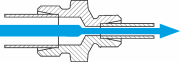
Pressure drop coefficient for reducers, reduction in direction of the flow
e.g.: C-RED, C-GR, C-KOVO
The pressure drop coefficient of extensions with an extension in direction of the flow is determined as follows:
| Exit opening (A₂) ⁄ Entry opening (A₁) | Pressure drop coefficient |
|---|---|
A₂ ⁄ A₁ = 0,8 | ζ = 0,15 |
A₂ ⁄ A₁ = 0,6 | ζ = 0,25 |
A₂ ⁄ A₁ = 0,4 | ζ = 0,35 |
A₂ ⁄ A₁ = 0,2 | ζ = 0,42 |
A₁ = cross section of the opening
A₂ = cross section of the exit
Pressure drop coefficient for banjo fittings
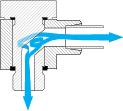
e.g.: C-WH-M, C-WH-R
The position of the internal screw has significant impact on the pressure drop coefficient.
The position of this internal screw cannot be predicted beforehand. Due to this the pressure drop coefficient is therefore specified as a possible range:
| Type | Pressure drop coefficient |
| C-WH | ζ = 3 ... 6 |
Pressure drop coefficient for manifolds
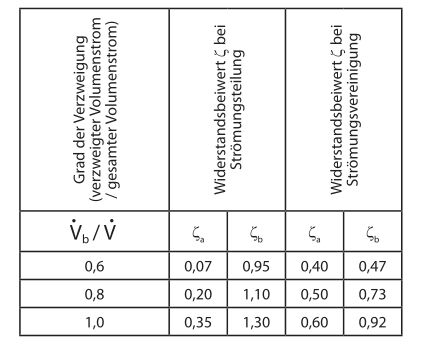
Pressure drop coefficient for manifolds
e.g.: C-K, C-TE, C-T, C-ET, C-EVT, C-EVL
With manifolds it depends on the fact wether the manifold is used in order to divide a flow or in order to join a flow.
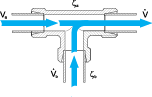
Straight direction of flow in the fitting

Dvision within the fitting
Pressure Drop Coefficient Elbow fitting
e.g.: C-W, C-EW
The drag coefficient may be assumed as following:
| Winkel-Verschraubung | ζ < 1 * |
* CONEXA fittings (like C-W) starting from sizes 10-L/12-S are without reduction of diameter.
Pressure drop coefficient for non-return valves
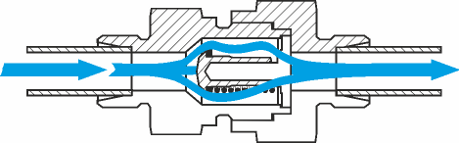
e.g.: C-RHD, C-RHDI, C-RHV, C-RHZ
The pressure drop coefficient for non-return valves in fully opened position can be assumed as follows:
Non-return valve | ζ = 5,0 |